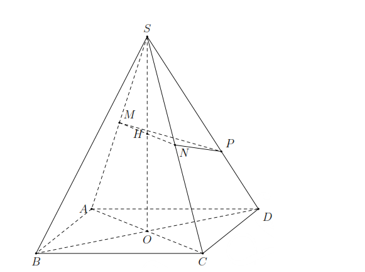
Chủ đề hình chóp đều: Hình chóp đều là một loại hình hấp dẫn với các đáy là các hình đa giác đều như tam giác đều hay hình vuông. Đặc biệt, tâm của đáy hình chóp trùng với chân đường cao, tạo nên sự cân đối và hài hòa cho hình. Ngoài ra, các mặt bên của hình chóp đều cũng là các hình tam giác đồng dạng, tạo nên sự đồng nhất và đẹp mắt cho hình.
Hình chóp đều có các đáy là đa giác gì?
Hình chóp đều có các đáy là các đa giác đều như tam giác đều, hình vuông, và các đa giác có number number số cạnh và number number góc phân chia đều. Mỗi cạnh của đa giác đều trong đáy giao cắt với mặt chóp tại một điểm và điểm này chung với đỉnh của hình chóp. Các đỉnh của đa giác trong đáy cũng liên kết với nhau thông qua các cạnh của đa giác để tạo thành các mặt bên của hình chóp.

Hình chóp đều là gì?
Hình chóp đều là một hình học có các đáy là đa giác đều như tam giác đều, hình vuông và có tâm của đáy trùng với chân đường cao của hình chóp. Đáy của hình chóp đều là một đa giác có các cạnh có cùng độ dài và các góc bằng nhau. Mặt bên của hình chóp đều là các hình tam giác cân bằng nhau có chung đỉnh. Đỉnh của hình chóp là điểm giao nhau của các đường thẳng đi qua các đỉnh của các tam giác mặt bên.
Hình chóp đều có những đặc điểm gì?
Hình chóp đều là một hình có các mặt bên là các hình tam giác cân bằng nhau có chung đỉnh. Đỉnh của hình chóp này được gọi là đỉnh của hình chóp đều. Mỗi mặt tam giác cân của hình chóp đều có cạnh đáy là một cạnh của đa giác đều, như tam giác đều, hình vuông và các hình đa giác đều khác.
Ngoài ra, hình chóp đều còn có các đường thẳng đi qua đỉnh và song song với các cạnh của đáy, được gọi là các đường phân giác. Như vậy, hình chóp đều có tất cả các đường phân giác đều bằng nhau. Tâm của đáy của hình chóp đều nằm trên đường cao của hình chóp và trùng với đỉnh của hình chóp đều.
Đặc điểm quan trọng khác của hình chóp đều là các mặt tam giác cân của nó có diện tích đều nhau. Diện tích các mặt tam giác cân của hình chóp đều được tính bằng công thức A = (cạnh đáy) * (chiều cao) /2, với A là diện tích mỗi mặt tam giác cân, cạnh đáy là độ dài các cạnh của đa giác đều và chiều cao là khoảng cách từ đỉnh đến đáy của hình chóp.
Vậy làm sao để đoán biết một hình chóp có phải là hình chóp đều hay không? Để hình chóp là một hình chóp đều, các cạnh bên của nó phải có độ dài bằng nhau và đáy của nó phải là một đa giác đều.
Đáy của hình chóp đều có thể là loại hình gì?
Đáy của một hình chóp đều có thể là một đa giác đều như tam giác đều, hình vuông, hình lục giác đều, hình ngũ giác đều, hoặc bất kỳ đa giác đều nào khác.
Tâm của đáy hình chóp đều được định nghĩa như thế nào?
Tâm của đáy hình chóp đều được định nghĩa là giao điểm của ba đường trung tuyến của đa giác đều trong trường hợp này. Ba đường trung tuyến là đường đi qua trung điểm của hai đỉnh của đa giác đều và đi qua đỉnh đối diện với đáy. Vì đáy của hình chóp đều được coi là một đa giác đều, đường trung tuyến của đỉnh đáy cũng là đường cao và trung tuyến duy nhất của đỉnh phía trên đáy. Tâm của đáy hình chóp đều được coi như là trọng tâm của đa giác đều và được coi là trung điểm của cả ba đỉnh của đa giác đều đó.

_HOOK_
Toán lớp 8 - Bài 7: Hình chóp đều và hình chóp cụt đều - Cô Phạm Thị Huệ Chi
Hãy khám phá một thế giới hình học thú vị với video về hình chóp đều. Tìm hiểu về cách vẽ, tính diện tích và tính thể tích của hình chóp đều và khám phá những ứng dụng thực tế của chúng trong cuộc sống hàng ngày.
Toán lớp 8 - Bài 7 - Hình chóp đều và hình chóp cụt đều
Bạn đã từng thắc mắc về hình chóp cụt đều? Xem video này và tìm hiểu cách vẽ, tính toán diện tích và thể tích của hình chóp cụt đều. Hãy khám phá những tính chất độc đáo của hình học này và áp dụng trong thực tế.
Tại sao tâm của tam giác đều cũng là tâm của hình chóp đều?
Có thể giải thích tại sao tâm của tam giác đều cũng là tâm của hình chóp đều như sau:
Trong hình chóp đều, đáy là đa giác đều, ví dụ như tam giác đều. Tâm của tam giác đều là giao điểm của ba đường trung trực, đường cao và trung đường của tam giác. Điều này có nghĩa là tâm của tam giác đều nằm trên cùng một đường thẳng với đỉnh và tâm của hình chóp đều.
Một cách khác để hiểu điều này là xem xét công thức để tính diện tích bề mặt của hình chóp. Diện tích bề mặt của hình chóp đều được tính bằng tổng các diện tích của các mặt bên, tức là các tam giác cân. Do các tam giác này có chung một đỉnh, đó chính là đỉnh của hình chóp, nên tâm của tam giác đều cũng là tâm của hình chóp.
Vì vậy, tâm của tam giác đều cũng là tâm của hình chóp đều do vị trí hình học của đỉnh và các tam giác cân trong hình chóp.
Chân đường cao của hình chóp đều có vai trò gì?
Chân đường cao của hình chóp đều có vai trò rất quan trọng trong việc tính toán và xác định các đặc điểm của hình chóp. Chân đường cao là đoạn thẳng nối từ đỉnh của hình chóp đến đáy và vuông góc với mặt phẳng đáy.
Vai trò chính của chân đường cao là tạo thành đường thẳng vuông góc với đáy, giúp xác định các hình vuông, tam giác, hay đa giác đều trong hình chóp. Ngoài ra, chân đường cao còn gặp các điểm quan trọng khác như tâm của hình vuông đáy, tâm của tam giác đáy, đỉnh của hình chóp.
Chân đường cao còn có vai trò quan trọng trong tính toán diện tích và thể tích của hình chóp đều. Hình chóp đều có diện tích bề mặt bằng tổng diện tích của các mặt bên plus diện tích đáy. Diện tích mặt bên được tính bằng công thức \"nửa chu vi đáy nhân chiều cao mặt bên\", trong đó n là số cạnh của đa giác đều đáy của hình chóp.
Thể tích của hình chóp đều được tính bằng công thức \"diện tích đáy nhân chiều cao chia 3\". Chiều cao cũng chính là độ dài của chân đường cao.
Với vai trò quan trọng trong việc xác định các đặc điểm và tính toán tphù hợp của hình chóp đều, chân đường cao là một yếu tố không thể thiếu khi nghiên cứu về hình học không gian.
Đường trung tuyến trong tam giác đều có đặc điểm gì?
Đường trung tuyến trong tam giác đều có một số đặc điểm quan trọng như sau:
1. Đường trung tuyến trong tam giác đều là đường nằm giữa đỉnh và trung điểm của cạnh đối diện.
2. Trong tam giác đều, đường trung tuyến cắt nhau tại một điểm duy nhất là tâm của tam giác.
3. Tam giác đều có 3 đường trung tuyến, và tất cả các đường trung tuyến đều dài bằng nhau và cùng độ dài với một nửa của các cạnh của tam giác.
4. Đường trung tuyến trong tam giác đều cũng là đường cao, đường phân giác và đường trực giao với cạnh đối diện.
5. Đường trung tuyến trong tam giác đều chia tam giác thành 6 tam giác đều nhỏ bằng nhau.
Tóm lại, đường trung tuyến trong tam giác đều không chỉ là một đường nằm giữa đỉnh và trung điểm của cạnh đối diện, mà còn có nhiều đặc điểm quan trọng khác mà giúp xác định cấu trúc và tính chất của tam giác đều.
Toán 8 - CT MỚI - Hình chóp tứ giác đều - Thầy Kenka
Hình chóp tứ giác đều là gì? Mời bạn xem video này để hiểu rõ về đặc điểm, cách vẽ và tính diện tích, thể tích của hình chóp tứ giác đều. Khám phá những ứng dụng thú vị của hình chóp tứ giác đều trong kiến trúc và công nghiệp.
Tâm của đa giác đều được xác định như thế nào?
Tâm của đa giác đều được xác định như sau:
1. Đối với tam giác đều: Tâm của tam giác đều là giao điểm của ba đường trung tuyến. Đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện.
2. Đối với hình vuông: Tâm của hình vuông là giao điểm của hai đường chéo. Đường chéo là đoạn thẳng nối hai đỉnh không kề nhau của hình vuông.
3. Đối với các đa giác đều khác có số cạnh nhiều hơn: Tâm của đa giác đều có thể xác định bằng cách kẻ đường trung trực cho mỗi cạnh của đa giác đến tâm của các cạnh kề.
Tóm lại, tâm của đa giác đều được xác định bằng cách tìm các đường trung tuyến, đường chéo hoặc đường trung trực và xác định giao điểm của chúng.

Hình chóp đều có bao nhiêu mặt bên?
Hình chóp đều có bao nhiêu mặt bên?
Hình chóp đều có các mặt bên là các hình tam giác cân bằng nhau có chung đỉnh. Vì vậy, số lượng mặt bên của hình chóp đều sẽ phụ thuộc vào số cạnh của đáy hình chóp.
- Nếu đáy là một tam giác đều: Hình chóp đều có 3 mặt bên.
- Nếu đáy là một hình vuông: Hình chóp đều có 4 mặt bên.
- Nếu đáy là một hình ngũ giác đều: Hình chóp đều có 5 mặt bên.
- Và cứ như vậy, số lượng mặt bên của hình chóp đều sẽ tăng lên tương ứng với số cạnh của đáy hình chóp.
Tóm lại, số mặt bên của hình chóp đều sẽ bằng số cạnh của đáy.
_HOOK_
Các mặt bên của hình chóp đều có các đặc điểm gì?
Các mặt bên của hình chóp đều có các đặc điểm sau:
1. Các mặt bên của hình chóp đều là các hình tam giác cân bằng nhau. Điều này có nghĩa là cạnh đáy của hình chóp và cạnh của các mặt bên đều có độ dài bằng nhau.
2. Các mặt bên có chung một đỉnh. Đỉnh này là điểm giao của các cạnh của các mặt bên và là điểm cao nhất của hình chóp.
3. Các mặt bên của hình chóp đều là các tam giác cân, có nghĩa là các cạnh và góc đối diện của các mặt bên cũng có độ dài và độ lớn bằng nhau.
4. Chân đường cao của hình chóp đi qua đỉnh và trùng với tâm của đáy của hình chóp.
5. Tất cả các mặt bên của hình chóp đều kề và cắt nhau tại các cạnh của hình chóp.
Đó là những đặc điểm chính của các mặt bên của hình chóp đều.
Toán 8 - CT MỚI - Hình chóp tam giác đều - Thầy Kenka
Bạn yêu thích hình chóp tam giác đều? Hãy xem video này để tìm hiểu sâu hơn về tính chất, đặc điểm và ứng dụng của hình chóp tam giác đều. Khám phá cách vẽ, tính diện tích và thể tích của hình chóp này và áp dụng vào những bài toán thực tế.
Đỉnh của hình chóp đều là gì?
Đỉnh của hình chóp đều là điểm trên hình chóp mà các cạnh bên cùng hướng về. Đỉnh này là điểm chung của các đường thẳng nối từ các đỉnh của đáy hình chóp đến đỉnh của hình chóp. Đối với hình chóp đều, đỉnh của hình chóp nằm trùng với chân đường cao, tức là điểm trùng với tâm của đáy hình chóp.
Mỗi mặt bên của hình chóp đều là loại hình gì?
Mỗi mặt bên của hình chóp đều là hình tam giác đều.
Đầu tiên, để hiểu về hình chóp đều, chúng ta cần biết rằng hình chóp đều là một loại hình có các đáy là đa giác đều như tam giác đều, hình vuông, hình ngũ giác đều,... Và tâm của đáy hình chóp trùng với chân đường cao.
Giống như các hình chóp khác, hình chóp đều có các mặt bên, nhưng ở đây, mặt bên của hình chóp đều là các hình tam giác đều. Điều này có nghĩa là tất cả các tam giác bên của hình chóp đều có cùng độ dài các cạnh và cùng độ dài các góc.
Vì vậy, mỗi mặt bên của hình chóp đều là một hình tam giác đều, có cùng độ dài các cạnh và cùng độ dài các góc.
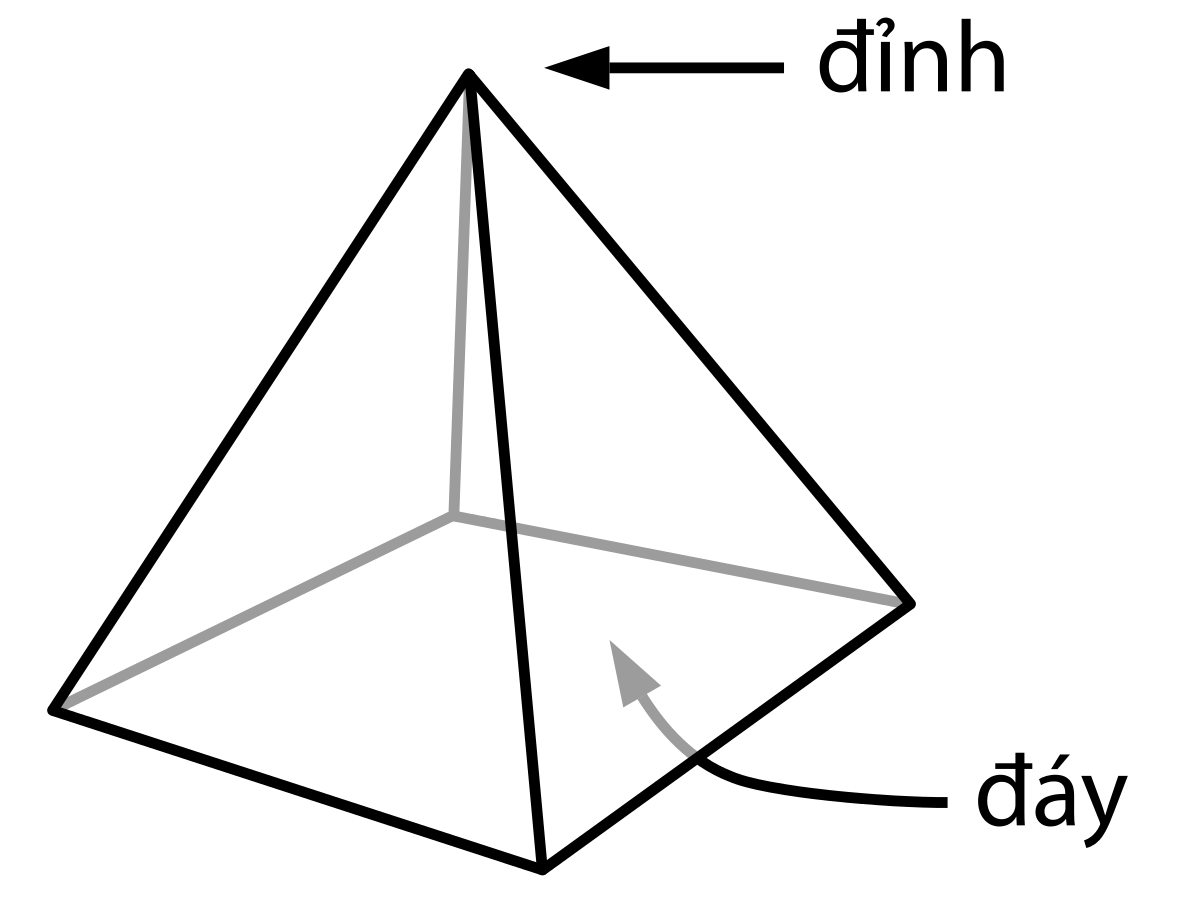
Các đường thẳng đi qua đỉnh của hình chóp đều có đặc điểm gì?
Các đường thẳng đi qua đỉnh của hình chóp đều có đặc điểm sau:
1. Đặc điểm chung của các đường thẳng đi qua đỉnh của hình chóp đều là chúng là đường cao của các mặt bên của hình chóp. Đường cao là đường đi từ đỉnh đến mặt đáy, và nằm vuông góc với mặt đáy của hình chóp.
2. Các đường thẳng đi qua đỉnh cũng là các đường trục của các mặt bên của hình chóp. Các mặt bên của hình chóp đều là các tam giác cân bằng nhau có chung đỉnh, và các đường thẳng đi qua đỉnh là các đường trục của các tam giác đó.
3. Ngoài ra, các đường thẳng đi qua đỉnh của hình chóp đều cắt mặt đáy của hình chóp tại các điểm đối xứng. Điểm đối xứng là điểm nằm ở phía đối diện và cách điểm đang xét qua đỉnh một khoảng cách bằng nhau.
4. Cuối cùng, các đường thẳng đi qua đỉnh của hình chóp đều cắt mặt đáy tạo thành các góc vuông. Điều này có nghĩa là các đường thẳng đi qua đỉnh là đường cao và đồng thời là đường trục của các tam giác đáy của hình chóp, nên chúng sẽ cắt mặt đáy tạo thành các góc vuông với mặt đáy.
Tóm lại, các đường thẳng đi qua đỉnh của hình chóp đều có các đặc điểm là là đường cao của các mặt bên, là các đường trục của các tam giác đáy, cắt mặt đáy tạo thành các điểm đối xứng và tạo thành các góc vuông với mặt đáy.
Tại sao hình chóp đều được coi là một hình học quan trọng trong toán học?
Hình chóp đều là một hình có đáy là một đa giác đều và các mặt bên là các tam giác đều có cùng kích thước. Điều này làm cho hình chóp đều trở thành một trong những hình học quan trọng trong toán học. Dưới đây là một số lý do tại sao hình chóp đều được coi là quan trọng:
1. Đối với hình học không gian: Hình chóp đều là một trong những hình học không gian cơ bản. Việc hiểu và áp dụng các khái niệm về hình chóp đều cho phép chúng ta nắm bắt được nhiều khía cạnh của không gian và tư duy về hình học không gian.
2. Liên quan đến các khái niệm khác: Hình chóp đều liên quan mật thiết đến các khái niệm như đáy đa giác đều, tam giác đều, mặt bên tam giác đều và nhiều khái niệm hình học khác. Việc hiểu rõ và áp dụng các khái niệm này giúp chúng ta phát triển tư duy logic và phân tích trong toán học.
3. Ứng dụng thực tế: Hình chóp đều có nhiều ứng dụng thực tế trong đời sống hàng ngày và các lĩnh vực khoa học khác. Ví dụ, các ngôi sao và kim tự tháp có thể được mô hình hoá bằng hình chóp đều. Ngoài ra, trong lĩnh vực kiến trúc và kỹ thuật, hiểu rõ về hình chóp đều giúp chúng ta thiết kế và xây dựng các công trình có mặt chóp đẹp và ổn định.
Với những lợi ích trên, hình chóp đều được coi là một hình học quan trọng trong toán học và có ứng dụng rộng rãi trong nhiều lĩnh vực.
_HOOK_